Matrix Multiplication

So far we only concentrated on square matrix multiplications. However, we are not limited to square matrices alone.

Lets look again at our image that represents the multiplication $P$ x $Q$ :

Remember, the order here does matter, as matrix multiplication is not commutative

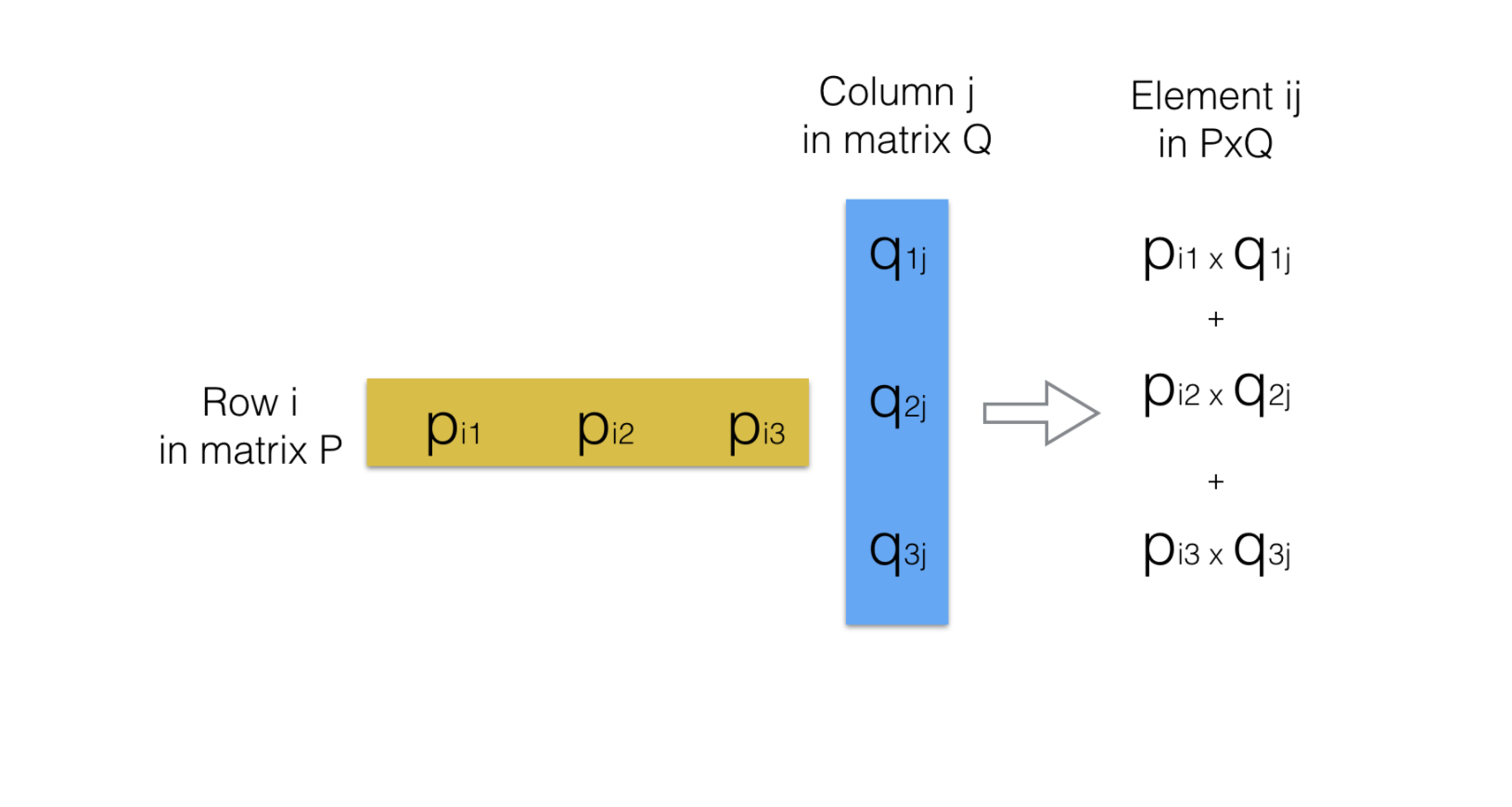
If you look closely at the image that represents the multiplication of $P$ x $Q$ , you will see that the number columns in $P$ equals the number of rows in $Q$ . (In the case of our example, it was $3$ ).

How many rows do we have in matrix $P$ ? How many columns do we have in matrix $Q$ ? That will deretmine the dimensions of the resulting multiplication.

In other words, if $P$ is a matrix with dimensions $t$ x $m$ and $Q$ is a matrix with dimensions $m$ x $v$ then:

$P$ x $Q$ is possible as the dimensions match. ( $P$ has $m$ columns and $Q$ has $m$ rows).
$P$ x $Q$ will be a matrix of $t$ x $v$ . ( $t$ rows and $v$ columns).

Lets look at an example:

$P=\begin{bmatrix} p_{11} &p_{12} &p_{13}\\ p_{21} &p_{22} &p_{23}\end{bmatrix}$

$Q=\begin{bmatrix} q_{11} &q_{12}&q_{13}&q_{14}\\ q_{21} &q_{22}&q_{23}&q_{24} \\q_{31} &q_{32}&q_{33}&q_{34}\end{bmatrix}$

We would like to calculate $P$ x $Q$ .

Our first step is to see if the calculation is possible. We will do that by looking at the dimensions of the matrices.

Matrix $P$ has $3$ columns and matrix $Q$ has $3$ rows. Perfect! multiplication is possible.

We expect to have a final result $P$ x $Q$ with the dimensions $2$ x $4$ ( $2$ rows and $4$ columns).

$P$ x $Q$ = $\begin{bmatrix} p_{11}q_{11}+p_{12}q_{21}+p_{13}q_{31} &p_{11}q_{12}+p_{12}q_{22}+p_{13}q_{32} &p_{11}q_{13}+p_{12}q_{23}+p_{13}q_{33} &p_{11}q_{14}+p_{12}q_{24}+p_{13}q_{34}\\ p_{21}q_{11}+p_{22}q_{21}+p_{23}q_{31} &p_{21}q_{12}+p_{22}q_{22}+p_{23}q_{32} &p_{21}q_{13}+p_{22}q_{23}+p_{23}q_{33}&p_{21}q_{14}+p_{22}q_{24}+p_{23}q_{34}\end{bmatrix}$

Equation 16